PARÁBOLAS

                               LAS PARÁBOLAS


Acabamos de empezar un nuevo , LAS PÁRABOLAS,  lo primero que queremos saber que son y como lo podemos diferenciar en nuestro entorno, incluso cuando nos miramos en el espejo, EMPEZAMOS CON LAS MATES.

1.1 ¿ Qué son las parábolas en mates?

Una parábola es una curva en la que los puntos están a la misma distancia de: un punto fijo (el foco) una línea fija (la directriz) 1.2 ¿Cómo podemos diferenciar un parábola?  Podríamos decir que newton fue el que descubrió las parábolas, gracias a la gravedad, y por qué digo esto, porque fácilmente cuando lanzamos un objeto al aire, este siempre baja, y podemos observar que ese objeto está haciendo una parábola. 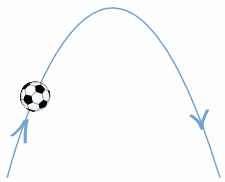En esta imagen podemos ver el lanzamiento de un balón, como podemos observar está haciendo una parábola    Nosotros vamos a utilizar un programa que es totalmente gratuito "GEOGEBRA" en la que podemos hacer todo con las mates.  Como estamos utilizando las mates, vamos a empezar: Yo elegí esta foto podemos ver con facilidad la parabola esta formula fue según geogebra : -((x-6,36)^2-6.51) y como dije antes que nos podíamos encontrar párabolas en nuestro rostro , aquí tenéis el ejemplo de Brad Pitt: La fórmula que utilicé para la barbilla es: (x-3,289)^2 +2,86 La fórmula que utilicé para la cabeza es: -(( x-3.26)^2 - 9,57) La fórmula de la nariz es: ((x - 3,3)^2 -5,74)    Como podéis ver en las imágenes hay parábolas diferentes, exactamente estas:        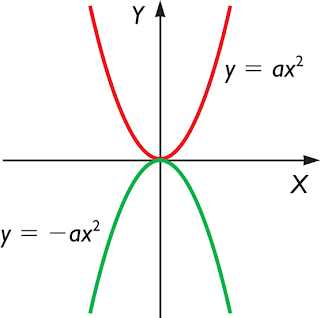Si a>0 ( positivo)  la parábola es cóncava, es decir la roja, por ejemplo x^2 Si a< 0 ( negativo) la párabola es convexa, es decir la verde , por ejemplo -x^2 ESPERO QUE LO HAYAN ENTENDIDO Y QUE  APRUEBENN, HASTA LA PRÓXIMAAA